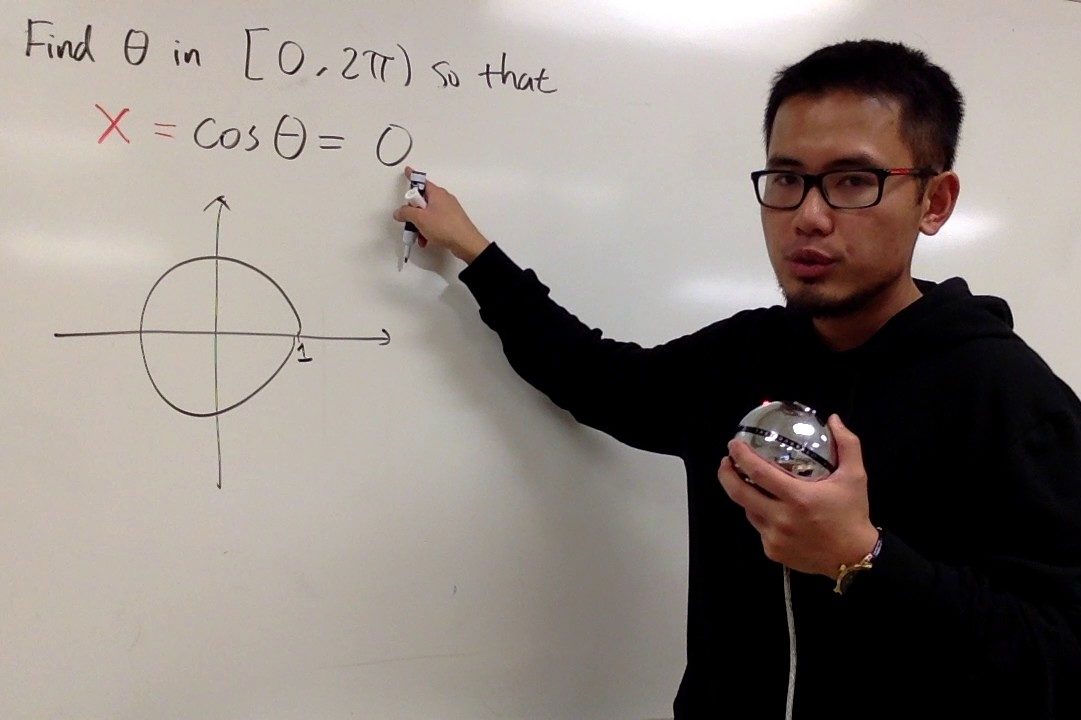Cos 0: If you want to know the value of cosine 0, this article will teach you how to calculate it. The relationship between sine and cosine is also discussed, as well as the Pythagorean theorem. Besides fundamental uses, the cosine and sine functions are also used in other applications, such as calculating angles. In addition to these, the cosine and sine functions are also useful in theoretical modeling.
Value of cos 0
A trigonometric function is a mathematical expression that relates angles and their lengths. In physics, this function is important for understanding the differences between two circles. The values of cosine are equal to the angle between a point on an x-axis and a point on a y-axis. Trigonometric functions are useful for determining the length of a triangle’s sides and are frequently used by navigators and engineers to measure average temperature variations.
Using a unit circle, you can calculate the cosine of any angle. A right-angled triangle has three sides, one opposite to the chosen angle and two adjacent sides. The other side is the hypotenuse. If these three sides are intersected at the intersection, the angle’s cosine is 0deg. Similarly, the opposite side of a right-angled triangle is called the hypotenuse, and the third side is the adjacent side.
In addition to the cosine of an angle, you can also calculate its period. The period is the distance between any point on a graph and the next matching point. For example, y=cos(x) has a period of 0.5 and an amplitude of 1. This is called the value of cosine 0.
Relationship between sine and cos 0
The definitions of the two trigonometry function sine and cosine are similar to each other, but there are some key differences. For example, the cosine of one angle equals the sine of the other. In other words, the cosine of one acute angle equals the sine of the other acute angle. In addition, both functions are at right angles, resulting in the inner product of their squares. This property is important for the Fourier series.
To calculate the complementary angles, use the sine and cosine relationship. These two functions are related to each other by the elliptic function E. The sine function gives the hypotenuse length of the opposite side of a triangle; the cosine function gives the hypotenuse length of the adjacent side. If the sine function is greater than the cosine function, the cosine will give a smaller length.
When using a graph, the cosine function has values in the range of 1 to -1. When applied to a graph, it will produce a “hill and valley” pattern, and applied to the inverse cosine function, the pattern repeats after intervals of the same length. To understand the difference between cosine and sine, use the graph below. Once you understand the difference between sine and cosine, you can use this equation in any other situation.
The formula for calculating cosine 0
If you’re looking for a formula for calculating cosine o, this article is for you! This formula has many properties that you will want to know. First of all, it is a reciprocal of the sine. The other two terms are sine and tangent. To learn more about the relationship between these two functions, keep reading! Here are some examples. Also, check out BYJU’s website for more information on trigonometric functions.
The cosine of a 90-degree angle is always -one minus the angle. This means the cosine is zero when divided by the angle’s hypotenuse. To calculate the cosine of an angle, you must define the triangle’s hypotenuse and two 90-degree angles. The length of a line whose hypotenuse is zero is equal to x/r. You can use a cosine calculator to check your answer.
Another useful application of the cosine function is in determining angles. A right-angled triangle has three sides: the hypotenuse side, the opposite side, and the adjacent side. The third side is the opposite side of the hypotenuse. Its length is the hypotenuse. Once you’ve defined these three sides, you can use the cosine formula to calculate the angles in a triangle.
Pythagorean theorem
The Pythagorean theorem states that the tangent and secant of a right triangle are the same lengths. This means that the tangent of one leg equals the length of the other leg and vice versa. In this way, the tangent and secant of any angle are the same lengths. In other words, the right triangle’s hypotenuse is a right triangle.
This proves the importance of the Pythagorean theorem. The Pythagorean theorem is a mathematical statement that demonstrates the right triangle’s relationship with a unit circle. The right triangle has a radius of 1 and the legs are square. Thus, the radius of the right triangle on a unit circle is also equal to the hypotenuse.
The unit circle has a radius of 1. A ray from the origin makes an angle with the X-axis at the corresponding arc, making the cosine of a given angle. If two rays intersect in this circle, then the cosine of a is the x coordinate of that intersection. This definition will be useful in many areas, including the study of harmonic oscillators, calculating average temperature variations, and more.
The Pythagorean theorem cos 0 is a useful tool in solving triangles. By using it, you can find the unknown part of a triangle, in terms of its known parts. In other words, the Pythagorean theorem solves the unknown angles in terms of the known ones.
Trigonometric functions
If you are a student of geometry, you may be familiar with the concept of the cosine and sinus functions, which are ratios of angles. These are often used for angles smaller than the right angle. They are also used to study periodic phenomena, Listed below are the definitions of these three functions and how to use them in your own calculations.
Examples
Cosine of zero degrees equals one in trigonometric mathematics. There are three ways to derive this value – two related to the geometric system, and one related to trigonometry. One approach considers the property between the lengths of the sides of a triangle. Another method considers the cos function in ratio form between the lengths of the sides. In trigonometric mathematics, the cosine of zero degrees equals one when the angle of a right triangle is zero radians.
Besides the definitions above, cos 0 has many applications in mathematics. For example, in calculating the angle of a right triangle, you can use cos 0 to solve an nth-degree angle. However, if you want to simplify things, you can always use cos 0.
Another way to find cos 0-degree is to use the unit circle. In this way, you can easily find out the inverse of any angle. Remember, cos 0 equals one. Once you have learned how to calculate it, you can apply it to any problem in your life. In math, cos 0 is an integral of a number that is one.